How To Find The Derivative Graph Of A Graph

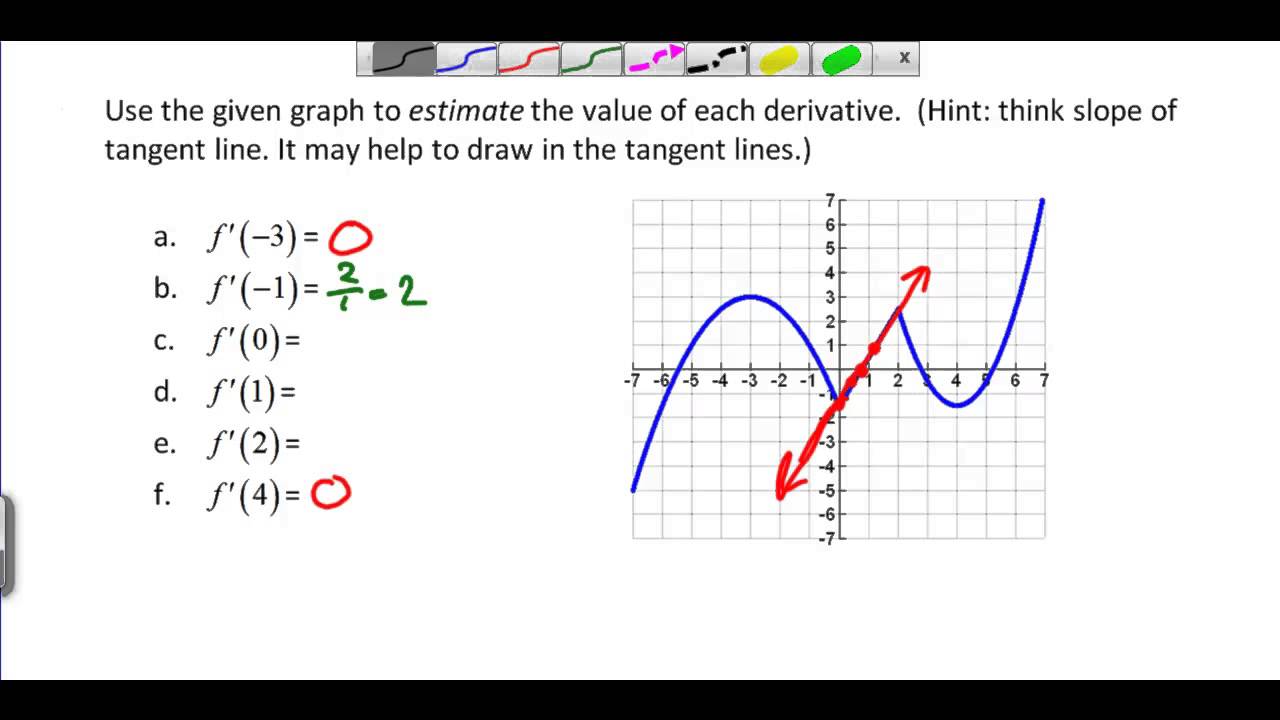
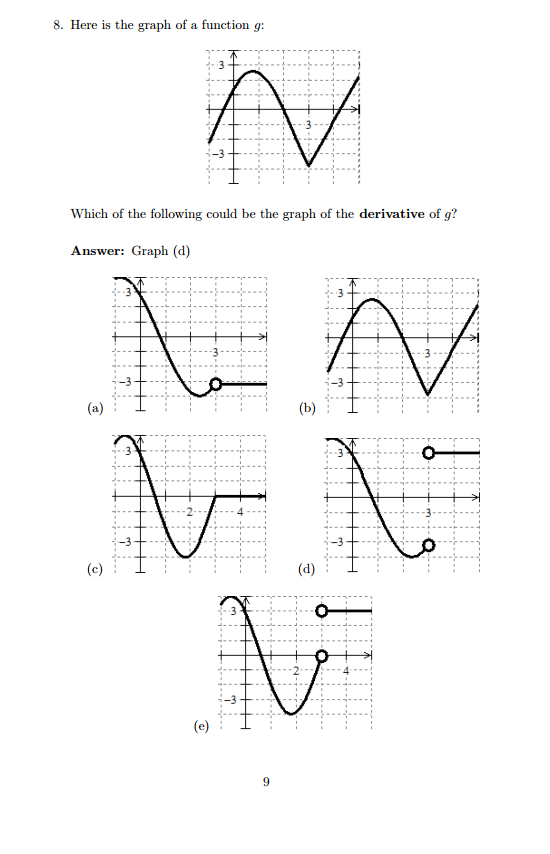
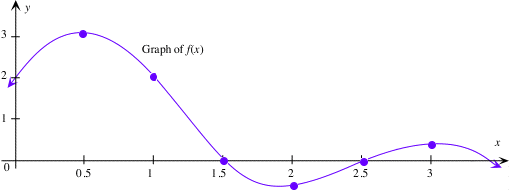
Example estimating the graph of a derivative.

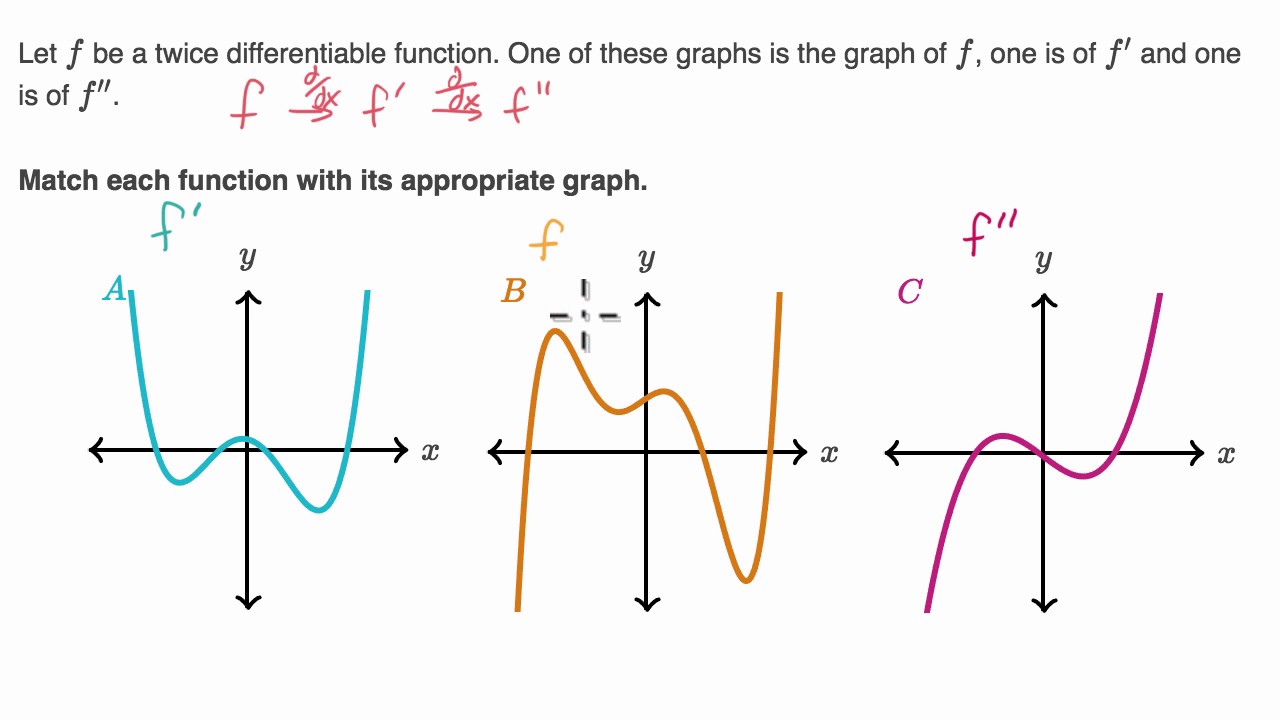
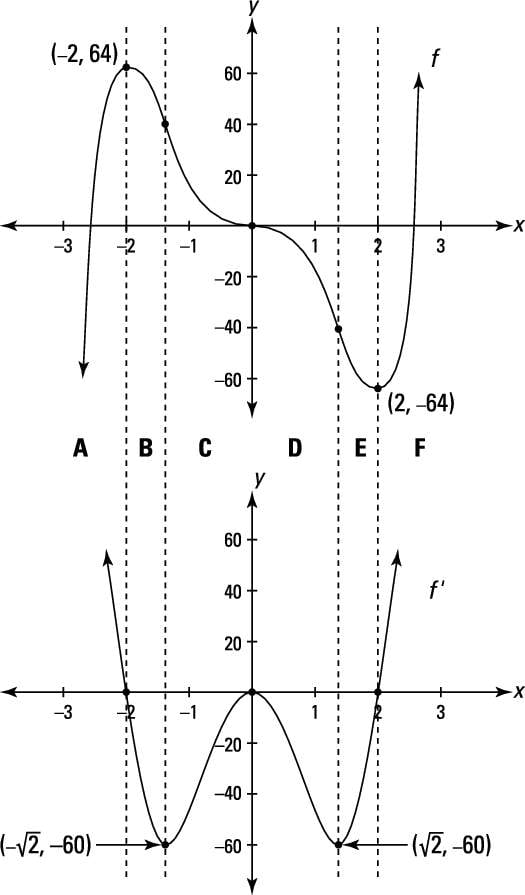
How to find the derivative graph of a graph. First identify the two turnaround points. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function s graph. At the value of the independent variable at which you want to evaluate the derivative draw a tangent. Explain the concavity test for a function over an open interval.

Use first and second derivative theorems to graph function f defined by f x x 2 solution to example 1. This means that f 2 f 0 0. When f is increasing we have f 0. Part 1 what comes to mind when you think of the word derivative.

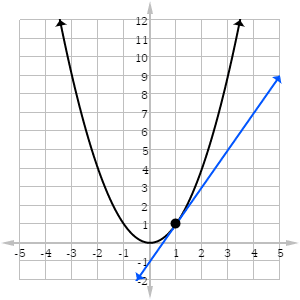
At the point i e. Draw a straight line tangent to the curve of the graph at this point. Find the first derivative any stationary points and the sign of f x to find intervals where f increases or decreases. Graph of graph of.

At x 2 and 0. If you don t want to mess up the paper or the graph is not on paper just position one edge of a ruler tangential to the. State the first derivative test for critical points. Choose a point on the graph to find the value of the derivative at.

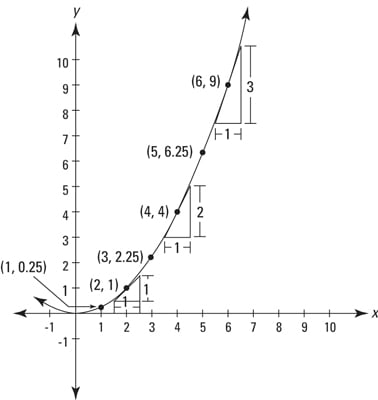
Then find and graph it. 1 graphing the derivative of a function warm up. Part 2 graph. Then identify the intervals on which the graph increases and decreases.