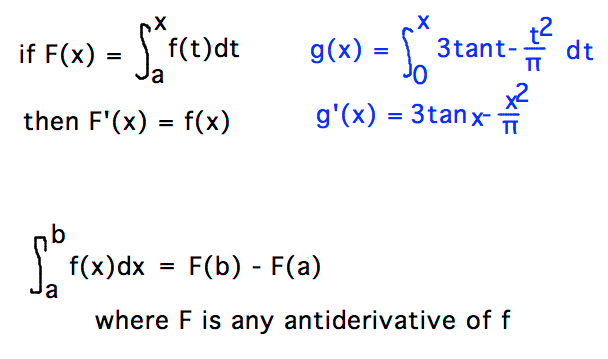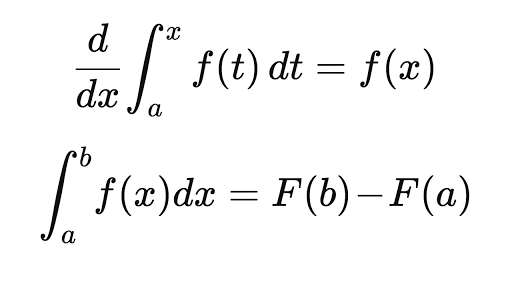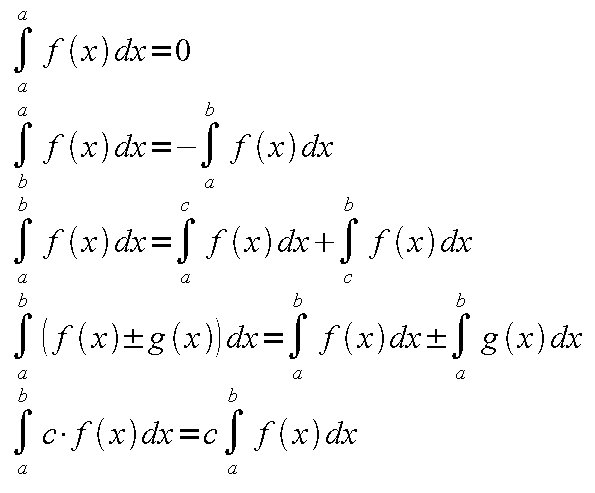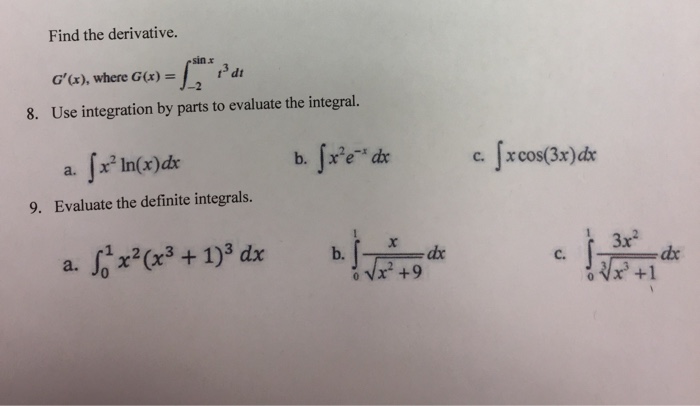How To Find The Derivative Of A Definite Integral
Taking Derivatives Of Integrals Youtube
Cpm Calculus 4 Review 13 The Derivative Of A Definite Integral
Derivatives Of Integrals W Chain Rule Youtube
Fundamental Theorem Of Calculus Derivatives Of Definite
Solved 1 Find The Derivative Of The Function H X 10
Differentiation Of Definite Integrals With Variable Limits Youtube
Let f x 3x 2.
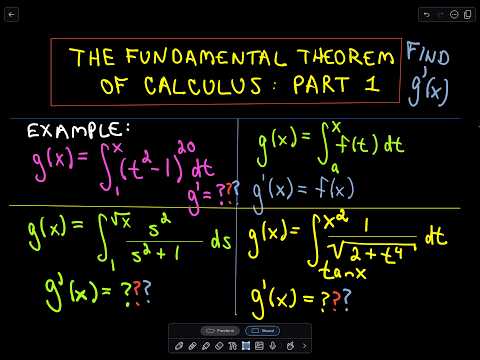
How to find the derivative of a definite integral. If you were to differentiate an integral with constant bounds of integration then the derivative would be zero as the definite integral evaluates to a constant. Type in any integral to get the solution free steps and graph this website uses cookies to ensure you get the best experience. That is the derivative of a definite integral of fwhose upper limit is the variable xand whose lower limit is the constant aequals the function fevaluated at x. And then finish with dx to mean the slices go in the x direction and approach zero in width.
It helps you practice by showing you the full working step by step integration. Our calculator allows you to check your solutions to calculus exercises. A definite integral has start and end values. Type in any integral to get the solution steps and graph this website uses cookies to ensure you get the best experience.
As expected the definite integral with constant limits produces a number as an answer and so the derivative of the integral is zero. In other words there is an interval a b. Using the restated fundamental theorem. To find an exact area you need to use a definite integral.
When you approximate the area under a curve the tops of the rectangles form a saw tooth shape that doesn t fit perfectly along the smooth curving function. It depends upon the definite integral in question. Compute the derivative of the integral of f x from x 0 to x t. After the integral symbol we put the function we want to find the integral of called the integrand.
Free integral calculator solve indefinite definite and multiple integrals with all the steps. Free definite integral calculator solve definite integrals with all the steps. The function named fis the same as the area function that was previously explored. You can approximate the area under a curve by adding up right left or midpoint rectangles.
The definite integral of a function on a given interval is defined as the area under the graph of the function inside the given. All common integration techniques and even special functions are supported. When talking about the derivative and a definite integral we need to talk about the fundamental theorem of calculus. This is true regardless of the value of the lower limit a.
Geneseo Math 221 10 Definite Integral Intro
Leibniz Integral Rule Wikipedia
Fundamental Theorem Of Calculus Review Article Khan Academy
Leibniz Integral Rule Wikipedia
Daily Report Calculus Formulas Finding Anti Derivatives
Derivative Of Definite Integral Conundrum Physics Forums
Solved Find The Derivative G X Where G X Integral
The Fundamental Theorem Of Calculus Area And The Definite Integral
Anti Derivatives Calculating Indefinite Integrals Of Polynomials
Differentiating An Integral Function Using Chain Rule Expii
Example Finding The Derivative Of A Function Defined As An
Use The Fundamental Theorem Of Calculus To Find The Derivative Of
Ex Evaluate A Definite Integral And The Derivative Of An Integral
Finding Derivative With Fundamental Theorem Of Calculus Chain
